Sovente gli astrofili visualisti fanno a gara nel risolvere stelle doppie molto strette. Ovvero cercare di separare due stelline, preferibilmente di uguale luminosità, a distanza apparente (o reale) reciproca molto ridotta. Così come in passato si utilizzavano le stelle doppie per testare la bontà della propria vista, oggi gli astrofili utilizzando stelle doppie strette per testare la qualità dei propri telescopi. La separazione minima θ tra due stelle, misurata in secondi d’arco, osservabile al vostro telescopio è detto potere risolutivo raggiunta dal vostro telescopio. Questo significa che voi riuscirete ad osservare al telescopio particolari ed oggetti di dimensioni angolari superiori a θ. E’ possibile conoscere a priori il valore del potere risolutivo? Purtroppo no dato che dipende dalla turbolenza atmosferica (seeing), dalla qualità ottica del vostro telescopio e dal limite di diffrazione. Il primo parametro infatti è difficilmente quantificabile a priori e dipende dal giorno e dal luogo di osservazione. Anche il secondo spesso non è quantificabile dato che ormai i telescopi sono prodotti industriali spesso diversi l’uno dall’altro. L’unico parametro quantificabile poiché dipende unicamente dalla natura stessa della luce è il limite di diffrazione. Se quindi ipotiziamo di avere ottiche perfette ed un cielo privo di turbolenza atmosferica, allora il potere risolutivo sarà determinato unicamente dal limite di diffrazione. Questo è quello che spesso prende il nome di potere risolutivo teorico o con abuso di notazione potere risolutivo.
Prima di determinare matematicamente θ ricordiamo che la diffrazione è un fenomeno fisico che si manifesta quando un’onda incontra un ostacolo sul proprio cammino. Questo diventa tanto più importante tanto più le dimensioni dell’ostacolo si avvicinano alla lunghezza d’onda λ dell’onda incidente. Nel caso in esame l’onda incidente è rappresentata dall’onda (piana in prima approssimazione) elettromagnetica emessa dalla stella, mentre l’ostacolo è l’ottica. Quello che succede è che l’onda elettromagnetica arrivando a ridosso del nostro telescopio si “spacca”. Un “pezzo” sta fuori dal telescopio ed un “pezzo” entra nel telescopio in perfetta analogia con quanto succede quando le onde del mare entrano in un molo. Sulla base delle teorie dell’elettromagnetismo la componente dell’onda che entra nel telescopio si comporta come una sovrapposizione di numerose onde sferiche che iterferiscono tra loro dando luogo all’immagine di diffrazione. Nel caso dei telescopi caratterizzati tutti dall’avere un’apertura circolare, l’immagine di diffrazione di una sorgente puntiforme posta all’infinito (una stella) è rappresentata da anelli concentrici luminosi detti disco di Airy. L’anello centrale (punto) è solitamente molto più luminoso dei secondari ed è quello che costituisce l’immagine della stella che osserviamo al telescopio (vedi Figura 1).
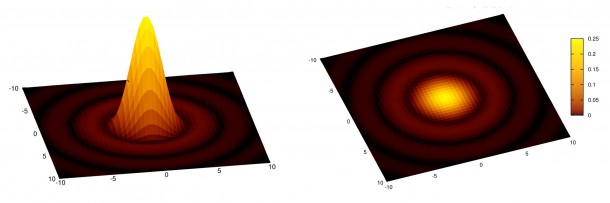
Figura1: immagine di diffrazione generata da una sorgente puntiforme. Sono ben visibili gli anelli luminosi intorno all'immagine della stella.
Cosa succede se ora abbiamo due stelle identiche molto vicine? Queste, rappresentate ciascuna dal proprio disco di Airy, andranno via via a sovrapporsi al diminuire della separazione angolare. Arriveremo ad un punto in cui le due stelle non sono più “separabili” ovvero non riusciamo più a distinguere separatamente i due dischi di Airy (vedi Figura 2). Tale distanza angolare sarà proprio il potere risolutivo teorico o limite di diffrazione. Si può dimostrare matematicamente che tale punto corrisponde alla distanza dal punto centrale del disco di Airy del primo anello di diffrazione (criterio di Rayleigh). Ecco quindi che abbiamo un modo per quantificare il potere risolutivo (teorico) del nostro telescopio.
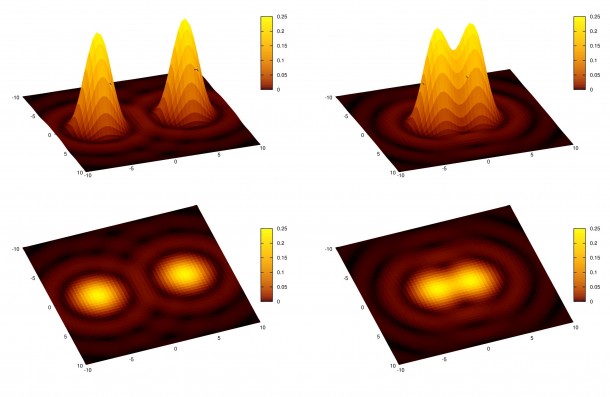
Figura 2: immagine di diffrazione generata da due sorgenti puntiformi. A sinistra quando sono lontane tra loro, a destra al limite di diffrazione.
Il limite di diffrazione e quindi il potere risolutivo teorico α dipenderà dalle dimensioni dell’ostacolo, ovvero dall’apertura del telescopio D, e dalla lunghezza d’onda della luce incidente λ. Mettendo tutto in formule:
α(rad) = 1.22 λ(nm)/D(nm)
per la luce visibile λ varia tra 380 e 760 nm. Un valore indicativo di 550nm risulta spesso più che adeguato dato che è la parte dello spettro elettromagnetico dove l’occhio umano e le reflex digitali sono più sensibili. D deve essere espresso in nm e quindi se voi conoscete il diametro del vostro telescopio in mm questo andrà moltiplicato per 1’000’000. Il risultato ottenuto sarà in radianti. Per trasformarlo in secondi d’arco dovrete moltiplicare il risultato ottenuto per 206’265. Come vedete il potere risolutivo teorico aumenta all’aumentare della lunghezza d’onda ed al diminuire del diametro del telescopio.
Purtroppo il termine “potere risolutivo” può generare giustamente confusione. Infatti se aumenta il potere risolutivo uno immagina che aumenta la capacità del telescopio di risolvere oggetti di piccole dimensioni. Ebbene è il contrario, un aumento del potere risolutivo significa un aumento dell’angolo minimo risolvibile attraverso il nostro telescopio e quindi un peggioramento della qualità della vostra ottica. Telescopi con bassi valori di potere risolutivo sono quindi migliori di telescopi con alto valore di potere risolutivo. Molto spesso quindi potrete leggere o sentir parlare di aumento del potere risolutivo con il diametro del telescopio ovviamente sbagliato dal punto di vista formale.
A titolo di esempio, un telescopio Newton 150mm avrà un potere risolutivo teorico pari a:
- Rosso (700 nm): 1.17 arcsec
- Verde (546.1 nm): 0.92 arcsec
- Blu (455.8 nm): 0.76 arcsec
Come detto in precenza a questo bisognerà aggiungere il contributo dovuto alla qualità dell’ottica. Questo è difficilmente valutabile ed è inferiore al limite di diffrazione solitamente per ottiche con rapporti focali f/ superiori a 8. Il contributo invece dovuto al seeing è solitamente compreso tra circa 0.4 arcsec (La Palma) ed i 2-3 arcsec o superiori nel caso di forte turbolenza atmosferica. E’ quindi facile notare come il limite di diffrazione possa talvolta non essere dominante nel calcolo del potere risolutivo di un telescopio.




1 commento
Il campionamento : ASTROtrezzi.it · Novembre 8, 2013 alle 10:29 am
[…] post “Il potere risolutivo“, abbiamo visto come la risoluzione delle nostre immagini astronomiche dipendano dalla […]