Il processo di calibrazione di uno spettro elettromagnetico è il primo passo per riuscire a dare una descrizione quantitativa di quanto acquisito per esempio con un reticolo di diffrazione come lo StarAnalyser 100. Per fare questo si è deciso di acquisire lo spettro di 9 stelle differenti di classe A. La scelta di questa classe spettrale deriva dal fatto che a quella temperatura sono ben visibili le linee della serie di Balmer dell’Idrogeno neutro HI, in grado con la banda tellurica dell’Ossigeno O2 a 7620 Å, di coprire l’intero spettro del visibile.
A questo punto la procedura seguita è la seguente:
- acquisizione dello spettro elettromagnetico della stella (file AVI) modificando tempi di esposizione e messa a fuoco al fine di ridurre eventuali errori sistematici;
- elaborazione del filmato AVI con Registax 6 al fine di ottenere l’immagine somma (file TIFF)
- rotazione dello spettro in modo da portarlo in posizione orizzontale. Selezione dello stesso ed espansione dell’immagine a 200 pixel di altezza;
- conversione del file TIFF in file PIC con IRIS;
- importazione del file PIC in Visual Spec, creazione dell’istogramma luminosità vs pixel in formato DAT;
- elaborazione di quest’ultimo con il software di analisi ROOT.
Per avere maggiori informazioni sui singoli passi riportati qui sopra fate riferimento agli altri post dedicati su ASTROtrezzi.
Obiettivo della calibrazione è trovare la relazione tra pixel e lunghezza d’onda λ della radiazione elettromagnetica. Fortunatamente per i reticoli di diffrazione questa relazione è in prima approssimazione di tipo lineare. Lunghezza d’onda zero corrisponde all’immagine dell’ordine zero della sorgente, ovvero nel nostro caso la stella in esame.
Quindi l’ideale sarebbe avere nel sistema di coordinate luminosità vs pixel come lunghezza d’onda zero il valore di pixel zero che in termini pratici si traduce nel porre la stella nell’origine del sistema di coordinate. Visual Spec purtroppo misura la distanza in pixel partendo dal lato sinistro dell’immagine che importiamo. Dato che la stella non è mai sul bordo, allora questa assumerà una posizione in pixel diversa da zero (offset). Per risolvere questo problema abbiamo fittato con una distribuzione gaussiana il picco di luminosità corrispondente all’immagine della stella in esame e shiftato lo spettro del valore medio di tale distribuzione (che dovrebbe coincidere con la posizione del centro della stella misurato in pixel). Dato che ogni stella in esame si troverà rispetto al lato sinistro dell’immagine acquisita ad una distanza diversa allora anche il relativo offset sarà differente. Di seguito riportiamo i valori degli offset per il campione di stelle utilizzato:
- 80 UMa (A5): 16.4 pixel
- ε UMa (A0): 17.2 pixel
- α Gem (A2): 19.4 pixel
- β Leo (A3): 24.3 pixel
- δ UMa (A3): 17.9 pixel
- β UMa (A1): 21.9 pixel
- ζ UMa (A0): 12.6 pixel
- γ UMa (A0): 29.8 pixel
- δ Leo (A3): 19.6 pixel
A questo punto tutti gli spettri hanno lo stesso offset e se volete potete sovrapporli. Da una rapida occhiata noterete che tutti i picchi della serie di Balmer stanno praticamente nella stessa posizione. Questo non è del tutto vero in quanto potrebbero esserci degli errori. Per prenderli correttamente in considerazione abbiamo pertanto determinato la posizione in pixel dei picchi Hα, Hβ, Hγ, Hδ, Hε, Hζ, Hη ed O2(7620 Å) per ogni stella in esame. I valori ottenuti nei singoli set di dati ed il valore medio con relativa incertezza statistica sono riportati in tabella:
Valore in pixel dei vari picchi di assorbimento ottenuti per mezzo di un fit gaussiano.
Ora non ci resta che riportare in un grafico il valore teorico delle lunghezze d’onda per la serie di Balmer (calcolabili analiticamente) e per la banda tellurica O2 approssimata ad un picco a λ = 7620 Å, in funzione del rispettivo valore misurato in pixel.
Un fit lineare del tipo y = mx permetterà di ottenere il valore sperimentale di m (dispersione del reticolo). Questo purtroppo non ha fornito risultati soddisfacenti portando ad errori sulla determinazione delle lunghezze d’onda spesso superiori a 30 Å. Si è quindi proceduto effettuando fit con polinomi di ordine sempre maggiore ottenendo al sesto grado un errore inferiore ai 10 Å. Questo ha il vantaggio di permettere misure precise di lunghezze d’onda, ma essendo un polinomio la relazione tra lunghezza d’onda e pixel perdeva di significato fisico per λ > 800 nm.
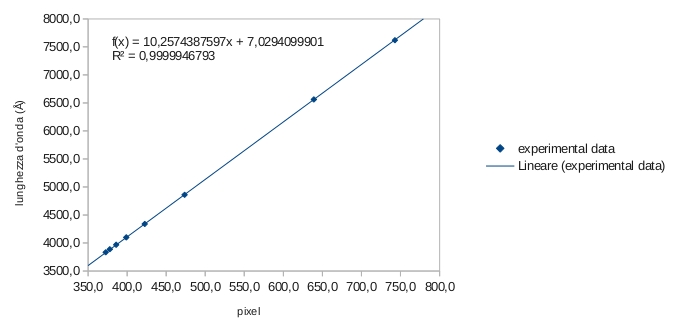
Dato che gli spettri acquisiti mostrano strutture anche per λ > 800 nm allora abbiamo abbandonato questa strada. Il risultato finale mostrato in figura è stato invece ottenuto utilizzando come curva di fit y = mx + q.
Determinazione della curva di calibrazione (fit lineare)
Il valore di q non nullo (comunque inferiore alla risoluzione dello strumento utilizzato) è da ricercarsi probabilmente in un offset intrinseco legato all’errore nella determinazione del centro della stella.
La curva di calibrazione che utilizzeremo per l’analisi degli spettri eseguiti con la strumentazione Newton SkyWather Wide Photo 200 mm f/4 + StarAnalyser 100 + camera Magzero MZ-5m è la seguente:
lunghezza d’onda = 10.2574387597*canale + 7.0294099901
Il massimo spred ottenuto tra i dati misurati e quelli teorici utilizzando questa curva di calibrazione è pari a 15.5 Å e sarà utilizzato come errore sulla misure effettuate. Un veloce test effettuato sulla stella αCMa ripresa con la medesima strumentazione mesi prima delle misure effettuate per la calibrazione mostra un accordo per la serie di Balmer e banda O2(7620 Å) con un errore inferiore ai 13.5 Å.
0 commenti